625. Расстояние между вершинами
Дан
неориентированный взвешенный граф. Найти вес минимального пути между двумя
вершинами.
Вход. Первая строка содержит натуральные числа n, m,
s и f (n ≤ 5000, m ≤ 100000, 1 ≤ s, f
≤ n, s ≠ f) – количество
вершин и ребер графа а также номера вершин, длину пути между которыми требуется
найти.
Следующие m строк
содержат по три натуральных числа bi,
ei и wi (1 ≤ bi,
ei ≤ n, 0 ≤ wi ≤ 100000) – номера концов i-ого ребра и его вес соответственно.
Выход. Первая строка
должна содержать вес минимального пути между вершинами s и f. Во второй строке
через пробел выведите вершины на кратчайшем пути из s в f в порядке обхода.
Если путь из s в f не существует, выведите -1.
|
Пример
входа |
Пример
выхода |
|
4 4 1 3 1 2 1 2 3 2 3 4 5 4 1 4 |
3 1 2 3 |
РЕШЕНИЕ
графы –
агоритм Дейкстры
Анализ алгоритма
Кратчайший путь
на взвешенном графе найдем при помощи алгоритма Дейкстры. Поскольку n ≤ 5000, то реализуем Дейкстру
при помощи кучи.
Пример
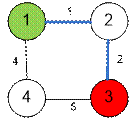
Граф,
приведенный в примере, имеет вид:
Реализация алгоритма
Определим макрос бесконечность.
#define INF 0x3F3F3F3F
Определим массив кратчайших расстояний dist и массив предков
par:
·
dist[i] хранит величину кратчайшего пути от истока до вершины i;
·
par[i] хранит
предка вершины i на кратчайшем пути
от истока до i;
vector<int> dist, par;
Определим структуру ребро, которая хранит информацию в какую
вершину оно направлено и его вес.
struct edge
{
int node,
dist;
edge(int
node, int dist) : node(node), dist(dist) {}
};
При занесении ребер в очередь с приоритетами на ее вершине
будет ребро с наименьшим расстоянием.
bool operator<
(edge a, edge b)
{
return a.dist
> b.dist;
}
Объявим структуру данных граф. Для каждой вершины i массив g[i] хранит список исходящих ребер.
vector<vector<edge>
> g;
Реализация алгоритма Дейкстры при помощи очереди с
приоритетами.
void
Dijkstra(vector<vector<edge> > &g, vector<int> &d, int
start)
{
Инициализируем очередь с приоритетами.
priority_queue<edge> pq;
pq.push(edge(start,0));
Инициализируем массив кратчайших расстояний.
d = vector<int>(n+1,INF);
d[start] = 0;
par = vector<int>(n+1,-1);
while(!pq.empty())
{
edge e = pq.top(); pq.pop();
int v =
e.node;
Пропускаем фиктивную вершину.
if (e.dist
> d[v]) continue;
Перебираем ребра, исходящие из вершины v.
for(int j = 0; j < g[v].size(); j++)
{
Из вершины v выходит ребро в
to с весом cost.
int to =
g[v][j].node;
int cost
= g[v][j].dist;
Проверяем релаксирует ли ребро.
if (d[v]
+ cost < d[to])
{
d[to] = d[v] + cost;
pq.push(edge(to,d[to]));
В случае релаксации кратчайший путь в to идет из v.
par[to] = v;
}
}
}
}
Основная часть программы. Читаем входные данные.
scanf("%d %d %d %d",&n,&m,&start,&fin);
g.resize(n+1);
Читаем ребра, строим граф.
for(i = 0; i < m; i++)
{
scanf("%d %d
%d",&b,&e,&w);
g[b].push_back(edge(e,w));
g[e].push_back(edge(b,w));
}
Запускаем алгоритм Дейкстры из вершины start.
Dijkstra(g,dist,start);
Если вершина fin не достижима, выводим -1.
if (dist[fin] == INF)
printf("-1\n");
else
{
Иначе выводим кратчайшее расстояние до вершины fin.
printf("%d\n",dist[fin]);
При помощи массива предков строим кратчайший путь.
for(i = fin;
i != -1; i = par[i])
res.push_back(i);
Выводим найденный кратчайший путь.
for(i =
res.size() - 1; i >= 0; i--)
printf("%d
",res[i]);
printf("\n");
}
Реализация алгоритма – пары
#include <cstdio>
#include <vector>
#include <queue>
#define INF 0x3F3F3F3F
using namespace std;
int b, e, w, v, j, i, tests;
int n, m, start, fin;
vector<int> dist, par, res;
vector<vector<pair<int, int>>> g;
void Dijkstra(vector<vector<pair<int, int>>>& g, vector<int>& d,
int start)
{
priority_queue<pair<int, int>, vector<pair<int, int>>,
greater<pair<int, int>>> pq;
pq.push({0, start});
d = vector<int>(n + 1, INF);
d[start] = 0;
par = vector<int>(n + 1, -1);
while (!pq.empty())
{
pair<int, int> e = pq.top(); pq.pop();
int v = e.second;
if (e.first > d[v]) continue;
for (int j = 0; j < g[v].size(); j++)
{
int to = g[v][j].first;
int cost = g[v][j].second;
if (d[v] + cost < d[to])
{
d[to] = d[v] + cost;
pq.push({ d[to], to });
par[to] = v;
}
}
}
}
int main(void)
{
//freopen("625.in", "r", stdin);
scanf("%d %d %d %d", &n, &m, &start, &fin);
g.resize(n + 1);
for (i = 0; i < m; i++)
{
scanf("%d %d %d", &b, &e, &w);
g[b].push_back({ e, w });
g[e].push_back({ b, w });
}
Dijkstra(g, dist, start);
if (dist[fin] == INF)
printf("-1\n");
else
{
printf("%d\n", dist[fin]);
for (i = fin; i != -1; i =
par[i])
res.push_back(i);
for (i = res.size() - 1; i
>= 0; i--)
printf("%d ", res[i]);
printf("\n");
}
return 0;
}